Análisis de series temporales II:
abortos otoñales
Artículo nº124 de Suis
En el número anterior dijimos que íbamos a introducir las series temporales y lo estudiaríamos en una época de abortos otoñales. Para recordar diremos que una serie temporal es una secuencia de datos medidos en determinados momentos y ordenados cronológicamente.
Estos datos pueden haber sido recogidos (o suceder) a intervalos iguales o desiguales (sin una cadencia regular). Veamos un ejemplo de cada caso:
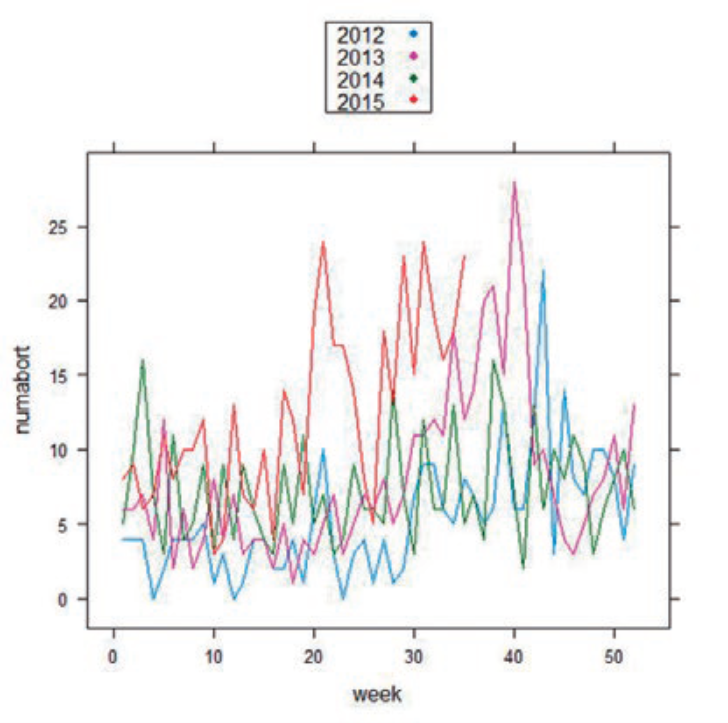
También en el número anterior hacíamos desde RCommander un gráfico que reproducimos aquí para ponernos en situación. Puede realizarse descargando el archivo “abortions.csv” de nuestro Drive. Una vez descargado, cargamos R, ejecutamos la instrucción library (Rcmdr) cargaremos los datos. Posteriormente, y en la pantalla de comandos de Rcmdr, ejecutamos el siguiente código (los símbolos # delante de cada línea son comentarios y no serán ejecutados por R).
#Ahora creamos dos nuevas variables a partir de las variables “week” y“year”, que son numéricas y tendremos “week2” y “year2” que serán factores (alfanuméricas)
Abortions$week2 <- as.factor(Abortions$week) Abortions$year2 <- as.factor(Abortions$year)
Y con ésta generamos el gráfico que aparecerá a continuación:
xyplot(numabort ~ week, groups=year2, type=”l”, pch=16,
auto.key=list(border=TRUE), par.settings=simpleTheme(pch=16),
scales=list(x=list(relation=’same’), y=list(relation=’same’)),
data=Abortions)
El modelo general de las series temporales
En este artículo damos un paso más y empezamos a analizar el modelo.
Una serie temporal de datos es la suma (modelo aditivo) de varias componentes que podemos presentar como:
Xt = Tt + St + It o Valor observado =
Tendencia + Estacionalidad + Irregular
donde,
Igual que con otros modelos, queremos estudiar las variables que influyen en él. En estos casos nos conviene aislar estos componentes de la serie. Una forma de estudiar la estacionalidad de una serie de datos es considerar cómo varía la media del periodo (del mes) respecto al periodo global. Con la siguiente tabla nos podemos hacer una idea de cómo se hacen los cálculos.
| Año 1 | Año 2 | … | Año N | Medias mensuales | Estacionalidad (S) | |
|---|---|---|---|---|---|---|
| Enero | x11 | x12 | … | x1n | µ1 | S1 |
| Fabrero | x21 | x22 | … | x2n | µ2 | S2 |
| … | … | … | … | … | … | … |
| Diciembre | x12 1 | x12 2 | … | x12 n | µ12 | S12 |
| Medias anuales | µ.1 | µ.2 | … | µ.n | µ… |
Donde:
Sacamos jugo a las series temporales con R
Vamos a intentar ver si nuestros datos tienen una tendencia estacional y lo vamos a hacer con R. Para ello, como ya tenemos cargado R, lo primero que haremos será cargar un paquete nuevo llamado “timeSeries”. Para ello iremos a la consola de R (donde cargamos habitualmente RCommander) y en Paquetes/Instalar paquete(s)… elegiremos un país que nos sirva de servidor (o espejo) y buscaremos cuando nos aparezca la pantalla de los paquetes, el paquete “timeSeries”.
Una vez instalado, cargaremos el archivo “abortionsmes.csv” que está en nuestro Drive.
A estos nuevos datos les llamaremos, cuando los importemos, “abortionsmes” para diferenciarlos de los que teníamos cargados antes (abortions). Verificaremos que los datos están cargados viendo que en RCommander, en la esquina superior izquierda, aparece la etiqueta “abortionsmes”. Estos datos son los mismos del archivo anterior pero agrupados mensualmente.
La función “descompose”
Para estimar las componentes de la tendencia y de la estacionalidad de un grupo de datos que pueden ser descritos usando un modelo aditivo (como el que tenemos), usaremos la función “decompose” del paquete “timeSeries”. Esta función estima la tendencia, la estacionalidad y la componente aleatoria de una serie temporal.
La función “decompose” devuelve un objeto de tipo lista donde las estimas de la componente de la tendencia, de estacionalidad y la aleatoriedad están almacenadas en unos elementos denominados “trend” para la tendencia, “seasonal” para la estacionalidad y “random” para la componente aleatoria.
Para poder llevar a cabo la función “decompose” primero cambiaremos el tipo de datos que tenemos cargados a un objeto “timeSeries” mediante la siguiente instrucción:
abortionsmesseries <- ts(abortionsmes, frequency=12, start=c(2012,1))
donde le decimos a R que nuestros datos “abortionsmes” son mensuales (frequency=12) y que comienzan en el año 2012, correspondiendo el primer dato a enero de 2012 [start=c(2012, 1)].
Después escribiremos en la pantalla de comandos de RCommander la siguiente instrucción:
abortimeseriescomponents <- decompose(abortionsmesseries)
Si ahora escribimos:
abortimeseriescomponents$seasonal,
R nos devolverá el siguiente grupo de datos:

Como vemos, las estimaciones para cada mes son las mismas para cada año. Podemos ver que el mayor factor estacional se da para los meses de septiembre y octubre de cada año.
Seguimos con R, pero en gráficos
Podemos verlo con un gráfico si escribimos:
Plot(abortimeseriescomponents)
con lo que obtenemos el siguiente gráfico:
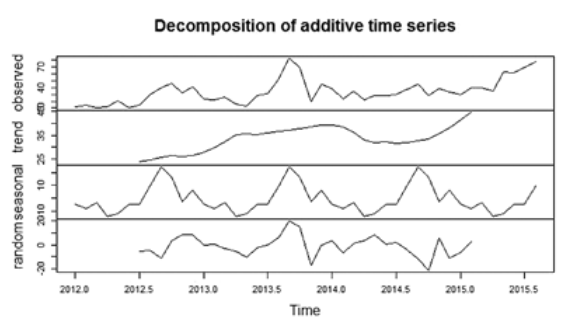
Descomposición de los factores aditivos de la serie temporal. Los “.0” son los meses de enero; los “.5” corresponden a los valores de julio. Así, se ve que los picos del gráfico correspondiente a “seasonal” tiene valores máximos en septiembre y octubre.
Vemos un efecto estacional (ver la parte “seasonal” de lal gráfico) en los meses de septiembre y octubre y también una tendencia a aumentar desde mediado del 2012 hasta el 2014, una tendencia a disminuir en casi todo el 2014 para volver a incrementarse hacia el final del 2014 y el inicio del 2015 (ver la parte “trend” del gráfico).
Volveremos sobre estas funciones y sobre más utilidades de la estacionalidad de datos en el siguiente número.