Análisis de series temporales I:
abortos otoñales
Artículo nº123 de Suis.
Iniciamos una serie de capítulos donde vamos a introducir el análisis de las series temporales. Las series temporales son un tipo de datos muy comunes en la producción animal. Por ejemplo, a modo de introducción y ya que estamos en otoño (época habitual de problemas de abortos), una serie temporal podría ser el número total de abortos que una granja de reproductoras ha sufrido semanalmente durante los últimos cuatro años.
Una serie temporal es una secuencia de datos medidos en determinados momentos y ordenados cronológicamente. Los datos pueden haber sido recogidos o suceder a intervalos iguales (en este caso, la semana y, como variable del suceso, el número de abortos en una granja cada semana, o el número total de lechones nacidos muertos) o desiguales, sin una cadencia regular (como la cantidad de un producto usado contra la diarrea neonatal).
Para el análisis de las series temporales se usan métodos que ayudan a interpretarlas y que permiten extraer información representativa sobre las relaciones subyacentes entre los datos de la serie. Permiten, en diferente medida y con distinta confianza, extrapolar o interpolar los datos. De tal manera, se puede predecir el comportamiento de la serie en momentos no observados, sean en el futuro (extrapolación pronóstica), en el pasado (extrapolación retrógrada) o en momentos intermedios (interpolación).
Las series temporales se usan para estudiar la relación causal entre diversas variables que cambian con el tiempo y se influyen entre sí. Muchas series temporales tienen una tendencia creciente (por ejemplo, el número de automóviles en uso en casi todos los países durante los últimos cincuenta años) o decreciente (por ejemplo, el número de personas que trabajan en la agricultura); otras no tienen tendencia (la luminosidad a horas sucesivas, que varía cíclicamente a lo largo de las 24 horas del día) y son estacionarias.
Los cuatro componentes de las series temporales
El análisis más clásico de las series temporales se basa en que los valores que toma la variable de observación son la consecuencia de cuatro componentes, cuya actuación conjunta da como resultado los valores medidos. Estos componentes son los siguientes:
Tendencia regular: La tendencia regular indica la marcha general y persistente del fenómeno observado (en nuestro caso, el número de abortos) y es una componente de la serie que refleja la evolución a largo plazo. Por ejemplo, la tendencia creciente de la ganancia media diaria, independientemente de que en un
mes concreto en una granja, por determinadas causas, haya una disminución de la misma.
Variación estacional: La variación estacional o variación cíclica regular es el movimiento periódico a corto plazo. Se trata de una componente causal debida a la influencia de ciertos fenómenos que se repiten de manera periódica en un año (las estaciones), una semana (los fines de semana) o un día (las horas puntas) o cualquier otro periodo (inferior a un año). Recoge las oscilaciones que se producen en esos periodos de repetición.
Variación cíclica: El componente de la serie que recoge las oscilaciones periódicas de amplitud superior a un año se define como variación cíclica. Se aprecia como movimientos normalmente irregulares alrededor de la tendencia que, a diferencia de las variaciones estacionales, tienen un periodo y amplitud variables, pudiendo clasificarse como cíclicos, cuasi cíclicos o recurrentes.
Variación aleatoria o ruido: La variación aleatoria o ruido es una variación accidental y de carácter errático, también denominada residuo, y no muestra ninguna regularidad (salvo las regularidades estadísticas). Estas variaciones son debidas a fenómenos de carácter ocasional: en nuestro caso podría ser debida a la entrada de nuevas enfermedades, al cambio en la genética de la granja o del suministrador de pienso. Son fenómenos que el modelo de los datos no pueden explicar.
Variación trasciente: La variación trasciente o accidental es de carácter errático y es debida a fenómenos aislados que son capaces de modificar el comportamiento de la serie (tendencia, estacionalidad de las variaciones cíclicas y aleatorias).
R y la utilidad de los gráficos en las series temporales
La representación gráfica de las series temporales es una herramienta de análisis muy útil porque permite obtener información de una forma muy sencilla a variables que no lo son tanto.
Cargar los datos en R
El archivo con los datos que hay que analizar se encuentra en nuestro drive. Primero cargaremos R y posteriormente, con la instrucción library (“Rcmdr”), cargaremos RCommander. A continuación cargaremos los datos del archivo “abortions.csv”. Este archivo tiene las columnas separadas por puntos y comas (;) y lo denominaremos “Abortos”. Una vez cargados los datos, los revisaremos. Podemos verlos haciendo clic en el botón “Visualizar conjunto de datos”, o bien yendo a Estadísticos/Resúmenes/Conjunto de datos activos, para comprobar que están correctamente cargados.
Damos forma al modelo en R
El archivo tiene cuatro variables. La variable “numabort” contiene el número de abortos que han ocurrido en una granja de forma semanal desde 2012, mientras que el resto de variables contienen la información temporal: la semana (“week”), el año (“year”) y la variable “weekyear”, que es la información de la semana y año en una sola variable.
En primer lugar realizaremos un análisis exploratorio de nuestros datos: vamos a Estadísticos/Resúmenes/Conjunto de datos activo y veremos un resumen de lo que tenemos.
Desde RCommander, crearemos dos nuevas variables (más adelante veremos su utilidad). Una nueva variable será “week2” y será igual a “week” pero en este caso no será numérica, sino factor (variable cualitativa). La segunda variable será “year2” y será igual a “year” pero también como factor y no numérica.
Para crear estas variables iremos a Datos/Modificar variables del conjunto de datos activo/Convertir variable numérica en factor… Se nos abrirá una ventana donde elegiremos la variable “week”, marcaremos que queremos que la nueva variable tenga los valores como números y asignaremos el nombre “week2” a la nueva variable.
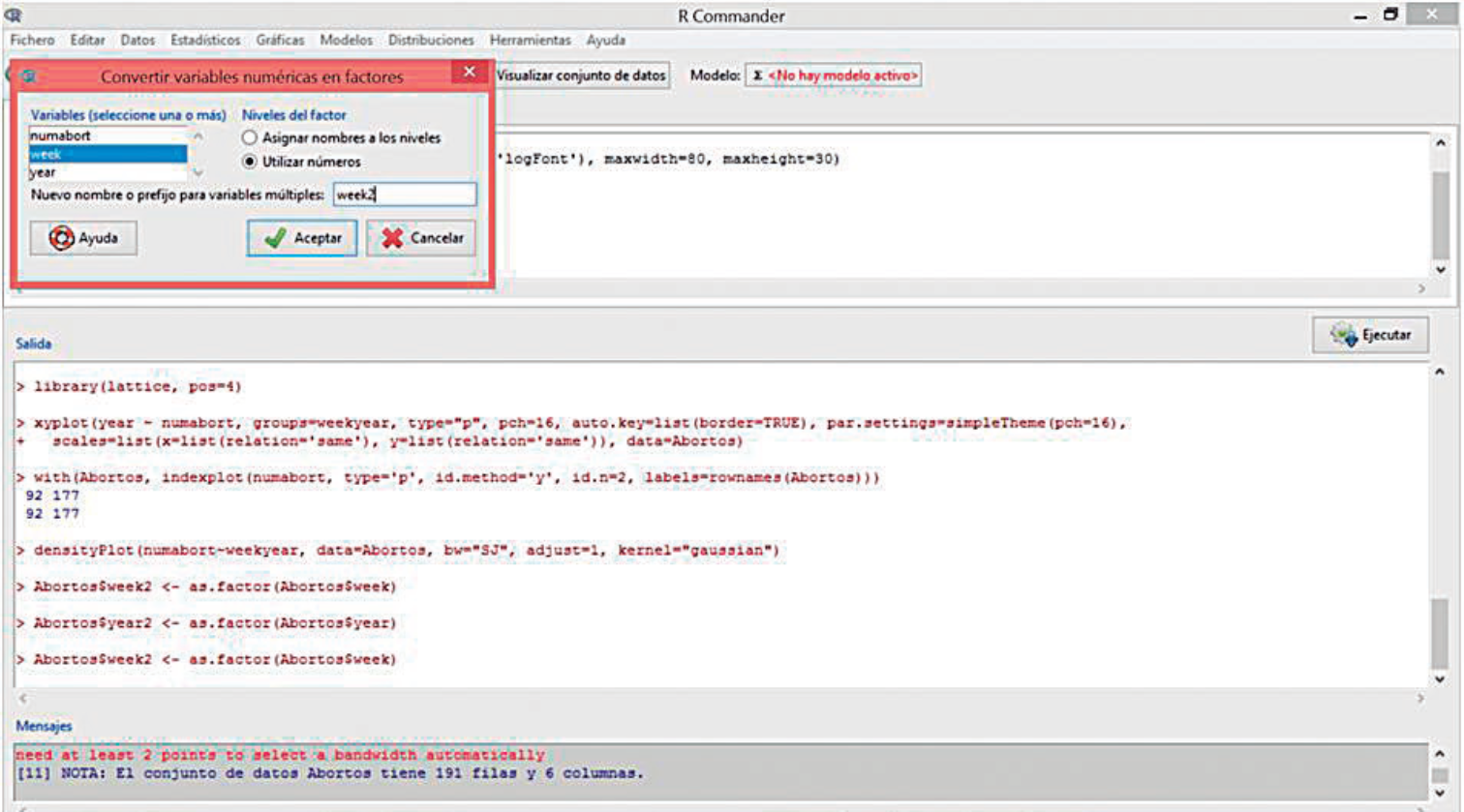
Haremos lo mismo con la variable “year” creando la variable “year2”.
Gráfico y quizá alguna conclusión
Podemos ejecutar ya un gráfico para ver “qué pintas tienen los datos” yendo a Gráficas/Graficas XY… Allí elegiremos en Variables explicativas la variable “week”, en Variables explicadas “numabort” y en Grupos “year2” (por esto la hemos creado como factor).
Si vamos a la pestaña Opciones y elegimos la opción Línea obtendremos el gráfico que se observa en la siguiente imagen.
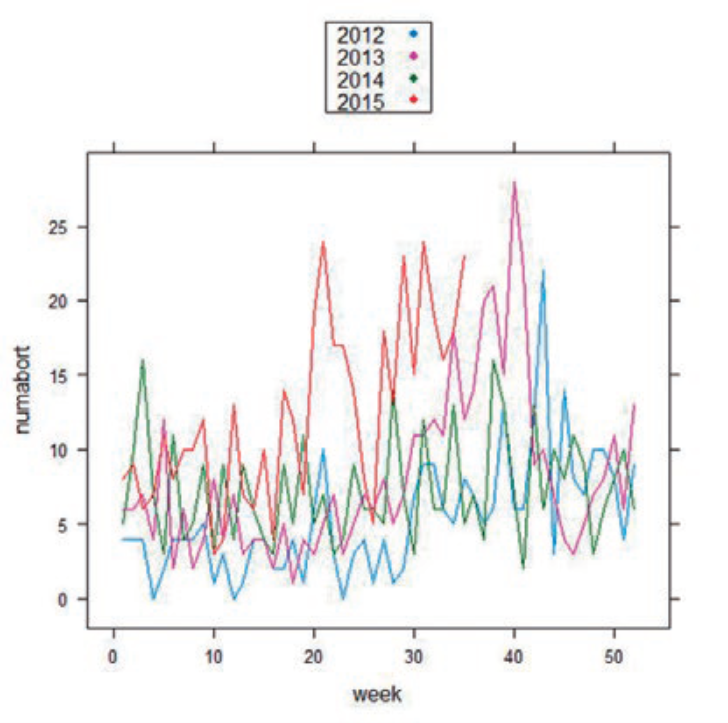
¿Podemos “ver” algo en este gráfico? ¿Existe un componente de estacionalidad? Comenzaremos a responder a estas cuestiones en el siguiente número.