¿Qué hacemos cuando tenemos dos medidas consecutivas de una variable en un sujeto?
El artículo publicado en el número 173 nos ha servido para darnos cuenta de que nunca en esta sección hemos tratado qué hacemos cuando en un sujeto (lechón, cerda, etc.) tenemos dos o más medidas de una variable separadas por intervalos regulares o no en el tiempo.
Por ejemplo, dos pesos: uno al nacimiento y otro al destete. O dos temperaturas: una al inicio de un proceso y otra al final. Y no solo debemos pensar en animales en cuanto a datos pareados: Imaginad una fábrica de pienso que mide la temperatura del pienso al entrar en la granuladora y al salir de ella. También son datos pareados que podemos definir como aquellos datos provenientes de muestras dependientes de los mismos individuos y responden a observaciones realizadas sobre esa muestra en momentos diferentes del estudio, ya sea antes y después de la aplicación de un tratamiento o sin introducir ningún tratamiento.
El análisis de los datos pareados se realiza de una forma especial. Veamos cómo hacerlo en un ejercicio práctico.
Primero descargamos los datos denominados “pareados” haciendo clic aquí . Para analizar los datos con R, cargaremos RCommander con library(Rcmdr) y cargaremos los datos en “Datos/ Importar datos/Desde un archivo Excel” eligiendo la Hoja 1. Lo denominaremos “pareados” y lo visualizaremos mediante la pestaña “Visualizar conjunto de datos” y veremos los datos de la tabla. En el artículo 86 explicamos detalladamente como hacer este primer paso.
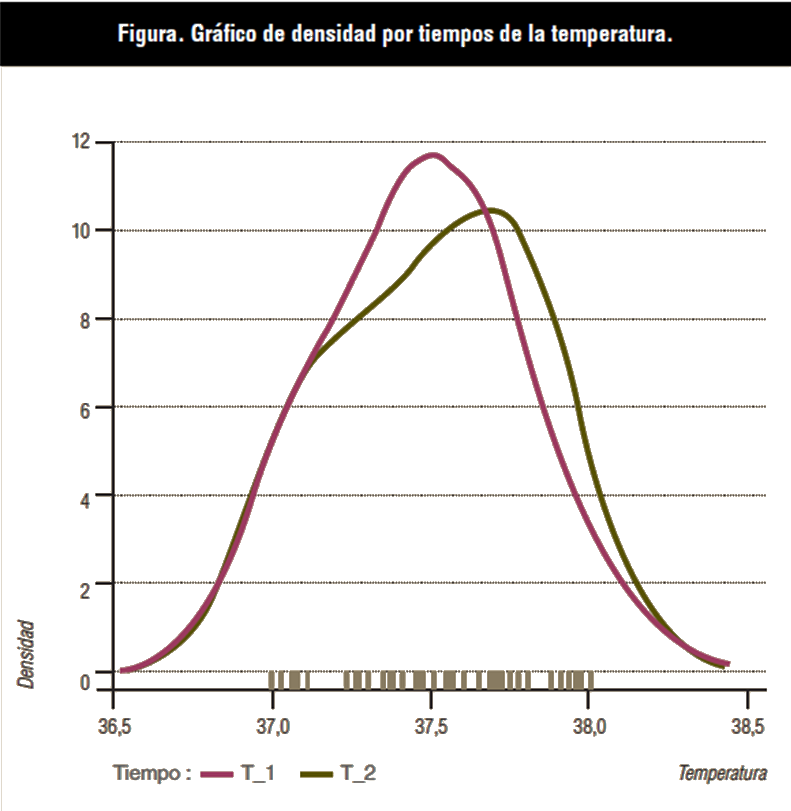
Los datos corresponden a las temperaturas de un grupo de 40 animales tomadas en dos momentos diferentes: T_1 y T_2, y para estudiar si existen diferencias usaremos un test t de Student que estudia las diferencias entre valores.
Lo primero que tenemos que hacer para aplicar un test t de Student es saber si los datos se distribuyen de forma normal. Para ello iremos a “Resúmenes/Test de normalidad”. Ya tenemos la variable problema seleccionada (temperatura) y yendo al botón “Test por grupos”, ya tendremos seleccionada la variable “tiempo”. La salida que obtendremos nos informará si las distribuciones de las temperaturas difieren de la distribución normal:
>normalityTest (temperatura ~ tiempo, test=”shapiro.test”, data=pareados) tiempo= T_1 Shapiro-Wilk normality test data: temperatura W = 0.95048, p-value = 0.07877 -------- tiempo= T_2 data: temperatura W = 0.93753, p-value = 0.02857
Podemos observar en la figura de la derecha que las temperaturas del tiempo T_2 no siguen la ley normal, pero para nuestro ejercicio, seguiremos considerándolas normales.
A continuación, debemos saber si las varianzas de las temperaturas en cada tiempo son iguales
Para ello, iremos a “Estadísticos/Varianzas/Test F para dos varianzas” y simplemente aceptando lo que por defecto tenemos, la variable “tiempo” como factor y la variable “temperatura” como dependiente, veremos que las varianza son iguales.
>var.test(temperatura ~ tiempo, alternative=’two.sided’, conf.level=.95, data=pareados) F test to compare two variances data: temperatura by tiempo F = 0.86409, num df = 39, denom df = 39, p-value = 0.6505 alternative hypothesis: true ratio of variances is not equal to 1 95 percent confidence interval: 0.4570171 1.6337530 sample estimates: ratio of variances 0.8640908
Ya podemos utilizar el t de Student
Para ello iremos a “Estadísticos/Medias/Test t para muestras independientes”. Y en la pestaña “Opciones”, elegiremos la opción “¿Suponer varianzas iguales?”. Elegiremos “Sí”, ya que lo hemos comprobado. Obtendremos:
>t.test(temperatura~tiempo, alternative=’two.sided’, conf.level=.95, var.equal=TRUE, data=pareados)
Two Sample t-test
data: temperatura by tiempo
t = -0.61728, df = 78, p-value = 0.5388
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval: -0.17534568 0.09234568
sample estimates: mean in tiempoT_1 mean in tiempoT_2
37.4735 37.5150Si supusiésemos que estas muestras fueran independientes, encontramos que las diferencias no son significativas (p-value = 0.5388) y el intervalo de la diferencia al 95 % de confianza está entre -0,18 y 0,09 ºC.
Si ahora importamos los datos del mismo fichero »pareados», pero de la Hoja 2 y lo denominamos “p2”, veremos que su estructuración es diferente.
¿Podríamos llegar a estos datos desde el primer fichero en R? Sí, existen varios métodos.
El paquete “reshape” nos ayuda a ello, pero en modo programación. Para cambiar los datos desde la estructura de la tabla del principio (formato conocido como “long”) a la tabla que acabamos de descubrir (formato conocido como “wide”), debemos escribir en la consola las siguientes instrucciones:
library(reshape) p2_new <- reshape(pareados, direction = “wide”, idvar = “id”, timevar = “tiempo”)
Si ahora elegimos el nuevo conjunto de datos “p2” veremos que ya tiene la estructura de la tabla.
Entonces vamos a ver el test t-Student, pero para datos pareados o dependientes, iremos a “Estadísticos/Medias/” y ya no nos aparecerá activada la opción de muestras independientes. Elegimos la opción de muestras relacionadas y elegimos en la primera variable la que aparece como temperatura T_1 y en la segunda la temperatura T_2.
Obtendremos:
>with(p2 (t.test(temperatura.T_1, temperatura.T_2, alternative=’two.sided’, conf.level=.95, paired=TRUE))) Paired t-test data: temperatura.T_1 and temperatura.T_2 t = -0.61871, df = 39, p-value = 0.5397 alternative hypothesis: true difference in means is not equal to 0 95 percent confidence interval: -0.17717183 0.09417183 sample estimates: mean of the differences -0.0415
Aquí vemos que el valor p es diferente del valor obtenido anteriormente y que la diferencia de las medias es de -0,0415 ºC.
Veamos un ejemplo con mayores diferencias
Los datos que utilizaremos para la realización de este caso están disponibles pinchando directamente aquí y se denominan »streams». Se han obtenido de un índice compuesto de biodiversidad que cuenta el número de invertebrados de una muestra de agua en dos tramos diferentes de un arroyo. Proviene del libro “The R book” (pág. 298).
Si los cargamos en RCommander veremos que hay dos variables: “up” y “down” que se refieren a la localización del arroyo donde se tomaron las muestras.
Con este formato RCommander no dos deja realizar un análisis t-Student como datos independientes. Si queremos ver las diferencias, lo tenemos que escribir con código. Si copiamos este código:
t.test(down, up)
y lo ejecutamos, obtendremos:
>t.test(down, up)
Welch Two Sample t-test data: down and up
t = -0.40876, df = 29.755, p-value = 0.6856
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval: -5.248256 3.498256
sample estimates: mean of x mean of y
12.500 13.375Si ahora lo hacemos mediante la opción (por defecto en RCommander) de datos relacionados o pareados obtendremos:
>with(streams (t.test(down, up, alternative=’two.sided’, conf.level=.95, paired=TRUE)))
Paired t-test
data: down and up
t = -3.0502, df = 15, p-value = 0.0081
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval: -1.4864388 -0.2635612
sample estimates: mean of the differences
-0.875Siendo completamente diferentes los resultados. Mientras que si los datos eran independientes no existía diferencia, ahora al tratarlos como relacionados o pareados, vemos que sí que existe una diferencia entre ellos.
En el próximo número seguiremos con estos ejemplos introduciendo otra idea y más variantes.
Si os ha surgido alguna duda durante la lectura y/o desarrollo de la actividad, no dudéis en contactar con nosotros y estaremos encantados de ayudaros.
Artículo número 175 publicado en Suis